Силы сопротивления

Формулы для расчета мощности тока

Измеряется электрическая мощность в ваттах (Вт). Ток в 1А и с напряжением в 1 В обладает мощностью в 1Вт. Для того, чтобы узнать, как определить мощность тока, необходимо воспользоваться следующей формулой: P=U*I (А), где U, I – это напряжение электрического поля и сила тока соответственно, а P – его мощность.

Чтобы понять, как правильно пользоваться формулой, рассмотрим небольшой пример. Допустим, подано напряжение на резистор в 150В и по нему идет ток в 0,2А. Какая на данном резисторе развивается мощность? P=150*0.2=30Вт.

Существует еще один способ вычисления мощности электрического тока. Если известно сопротивление цепи и сила тока, то необходимо воспользоваться законом Ома (применима формула для участка цепи): U=I*R (Б)

Теперь подставим формулу (Б) в формулу (А) и получим формулу (В): P=I 2 R (В). Предположим, что через реостат, сопротивление которого равно 5 Ом, проходит с силой 0,5А ток. Определить мощность, которая теряется в реостате? P=0.5 2 *5=1.25Вт.

Если сила тока нам неизвестна, но мы знаем напряжение и сопротивление, то тоже возможно определить мощность. Из закона Ома I=U/R, тогда пользуясь формулой (А) мощность тока равна: P=U 2 /R (Г)

Реостат имеет сопротивление в 5 Ом, а напряжение в нем 2,5В, тогда мощность согласно формуле (Г) будет равна: P=2.5 2 /5= 1.25Вт. Если вам известны любые два значения из формулы для закона Ома (если рассмотреть участок цепи), то всегда можно определить мощность тока.

Вспомнив определение мощности, можно записать еще одну формулу для её расчета: P=A/t (Д), где P – это мощность, А – работа электрического тока, а t – время, за которое совершается эта работа.

Выбирая тот или иной бытовой прибор в магазине, мы часто задаемся вопросом о том, сколько же денег нам придется заплатить за его использование. Особенно это касается обогревателя, работающего на электричестве. Иногда, пользуясь сварочным аппаратом или электродвигателем, мы даже не подозреваем о том, сколько он потребляет электроэнергии. Но как же узнать необходимые нам цифры, если данные о приборах не известны.

Движение тела, брошенного вертикально вверх

Аналогично можно рассмотреть движение тела, брошенного вертикально вверх с определенной начальной скоростью. Например, мы бросаем вверх мячик.

Пусть ось координат направлена вертикально вверх из точки бросания тела. На сей раз тело движется равнозамедленно, теряя скорость. В наивысшей точки скорость тела равна нулю. Применяя формулы кинематики, можно записать:

v=v-gt.

Подставив v=, найдем время подъема тела на максимальную высоту:

t=vg.

Время падения совпадает со временем подъема, и тело вернется на Землю через t=2vg.

 Максимальная высота подъема тела, брошенного вертикально:

h=v22g.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Взглянем на рисунок ниже. На нем приведены графики скоростей тел для трех случаев движения с ускорением a=-g. Рассмотрим каждый из них, предварительно уточнив, что в данном примере все числа округлены, а ускорение свободного падения принято равным 10мс2.

Первый график — это падение тела с некоторой высоты без начальной скорости. Время падения tп=1с. Из формул и из графика легко получить, что высота, с которой падало тело, равна h=5м.

Второй график — движение тела, брошенного вертикально вверх с начальной скоростью v=10 мс. Максимальная высота подъема h=5м. Время подъема и время падения tп=1с.

Третий график является продолжением первого. Падающее тело отскакивает от поверхности и его скорость резко меняет знак на противоположный. Дальнейшее движение тела можно рассматривать по второму графику.

Рассмотрим, как работает измеритель мощности в розетку

Если вам необходимо узнать, какой мощностью обладает тот или иной предмет, можно замерять с помощью прибора мультиметра силу тока и напряжение, а затем их просто перемножить. Есть и приборы, которые определяют и мощность. Они называются ваттметры. Показатель мощности рассчитывает встроенный калькулятор, и показатель сразу появляется на его дисплее.

Как пользоваться ваттметром и мультиметром:

1. Вставляем прибор в розетку 220В;
2. В ваттметр вставляем вилку прибора, который нам нужно замерять;
3. Ждем, когда на дисплее появится требуемый показатель.

На задней панели прибора есть отсек под батарейки, идущие обычно в комплекте. На пластине рядом имеется информация с характеристиками самого ваттметра, его номер, а также вилка. На внешней стороне находится дисплей. Управление осуществляется 4 кнопками, возле которых размещена розетка для подключения бытовых приборов, оборудования и техники.

С помощью четвертой кнопки Value вы сможете переключить и определить следующие измеряемые параметры:

• Напряжение сети;
• Мощность, которую потребляет подключенное устройство;
• Потребляемая прибором сила тока.

При установленном граничном показателе, относительно напряжению и току, одной из характеристик прибор будет давать сигнал. Это означает перегрузку.

Формулы для расчетов

Существуют формулы, с помощью которых можно рассчитывать различные показатели, связанные со свободным падением. В них используются такие условные обозначения:

1. u — конечная скорость, с которой перемещается исследуемое тело, м/с;
2. h — высота, с которой перемещается исследуемое тело, м;
3. t — время перемещения исследуемого тела, с;
4. g — ускорение (постоянная величина, равная 9,8 м/с2).

Формула для определения расстояния, пройденного падающим предметом при известной конечной скорости и времени падения: h = ut /2.

Формула для расчета расстояния, пройденного падающим предметом по постоянной величине g и времени: h = gt 2/2.

Формула для определения скорости падающего предмета в конце падения при известном времени падения: u = gt .

Формула для расчета скорости предмета в конце падения, если известна высота, с которой падает исследуемый предмет: u = √2 gh.

Ускорение свободного падения

Проводя свои знаменитые опыты на Пизанской башне Галилео Галилей выяснил, что все тела, независимо от их массы, падают на Землю одинаково. То есть, для всех тел ускорение свободного падения одинаково. По легенде, ученый тогда сбрасывал с башни шары разной массы.

Ускорение свободного падения

Ускорение свободного падения — ускорение, с которым все тела падают на Землю. 

Ускорение свободного падения приблизительно равно 9,81 мс2 и обозначается буквой g. Иногда, когда точность принципиально не важна, ускорение свободного падения округляют до 10 мс2.

Земля — не идеальный шар, и в различных точках земной поверхности, в зависимости от координат и высоты над уровнем моря, значение g варьируется. Так, самое большое ускорение свободного падения — на полюсах (≈9,83 мс2), а самое малое — на экваторе (≈9,78 мс2).

Когда сила Архимеда не работает

• Если тело плотно прилегает к поверхности. Если между телом и поверхностью нет жидкости или газа — нет и выталкивающей силы. Именно поэтому подводным лодкам нельзя ложиться на илистое дно — мощности их двигателей не хватит, чтобы преодолеть давление толщи воды сверху.
• В невесомости. Наличие веса у жидкости или газа — обязательное условие для возникновения архимедовой силы. В состоянии невесомости горячий воздух не поднимается, а холодный не опускается. Поэтому на МКС создают принудительную конвекцию воздуха с помощью вентиляторов.
• В растворах и смесях. Если в воду налить спирт, на него не будет действовать сила Архимеда, хотя плотность спирта меньше плотности воды. Поскольку связь между молекулами спирта слабее, чем связь молекул воды, он растворится в воде, и образуется новая жидкость — водный раствор спирта.

Суммарное сопротивление

Является суммой всех видов сил сопротивления:

X=X+Xi{\displaystyle X=X_{0}+X_{i}}

Так как сопротивление при нулевой подъёмной силе X{\displaystyle X_{0}} пропорционально квадрату скорости, а индуктивное Xi{\displaystyle X_{i}} — обратно пропорционально квадрату скорости, то они вносят разный вклад при разных скоростях. С ростом скорости X{\displaystyle X_{0}} растёт, а Xi{\displaystyle X_{i}} — падает, и график зависимости суммарного сопротивления X{\displaystyle X} от скорости («кривая потребной тяги») имеет минимум в точке пересечения кривых X{\displaystyle X_{0}} и Xi{\displaystyle X_{i}}, при которой обе силы сопротивления равны по величине. При этой скорости самолёт обладает наименьшим сопротивлением при заданной подъёмной силе (равной весу), а значит, наивысшим аэродинамическим качеством.

Мощность, требуемая для преодоления силы паразитного сопротивления, пропорциональна кубу скорости, а мощность, требуемая для преодоления индуктивного сопротивления, обратно пропорциональна скорости, поэтому суммарная мощность тоже имеет нелинейную зависимость от скорости. При некоторой скорости мощность (а значит, и расход топлива) становится минимальной — это скорость наибольшей продолжительности полёта (барражирования). Скорость, при которой достигается минимум отношения мощности (расхода топлива) к скорости полёта, является скоростью максимальной дальности полёта или крейсерской скоростью.

Сила — сопротивление

Сила сопротивления, направленная противоположно относит, перемещению тела, наз. Наиб, значение сила трения имеет в момент тро-гания тела с места. Различают трение скольжения и трение качения. Сила трения качения обычно значительно меньше силы трения скольжения.
 

Сила сопротивления вызывает увеличение натяжения тягового элемента на каждом участке.
 

Картина движения при поперечном обтекании пи-линдра.

Сила сопротивления складывается из двух частей: сопротивления трения и сопротивления формы. Сопротивление формы ( или, как его иначе называют, сопротивление давления) связано с явлениями срыва струй и образованием за обтекаемым телом зоны обратной циркуляции.
 

Обшая схема конвейерной линии.

Сила сопротивления вызывает увеличение натяжения тягового элемента на каждом участке.
 

Сила сопротивления ц считается постоянной по длине нити.
 

Схема механизма передвижения с гибкой тягой.

Сила сопротивления передвижению тележки в период установившегося движения состоит из силы трения W, ветровой нагрузки WB, разности сил в подъемных канатах А5, силы Я от провисания тягового каната или цепи, составляющей силы тяжести WyKji на уклоне.
 

Сила сопротивления, действующая на отдельную аэрозольную частицу, в основном возникает в результате различия скоростей частицы и обтекающего ее потока. Поэтому хаотическая скорость каждой частицы, обусловленная тепловым движением ее молекул, крайне мала.
 

Сила сопротивления, действующая на несферическую частицу, зависит от формы и ориентации частицы по отношению к направлению движения. В области действия закона Стокса частица обычно сохраняет свою первоначальную ориентацию во время осаждения, в то время как в области действия закона Ньютона она обычно принимает положение соответствующее максимальному сопротивлению. Коэффициенты сопротивления для дисков ( плоская сторона перпендикулярна направлению движения) и для цилиндров ( бесконечной длины с осью, перпендикулярной направлению движения) определяются по рис. П-67 как функция числа Рейнольдеа.
 

Сила сопротивления при относительном перемещении одного тела по поверхности другого под действием внешней силы, тангенциально направленная к общей границе между этими телами, называется силой трения.
 

Сила сопротивления fc пропорциональна квадрату скорост.
 

Схема сил, действующих.

Сила сопротивления стружкообразованию R3, действующая на заднюю поверхность инструмента, может быть представлена соответственно силами Руп, Р п л ( направленными нормально к площадке износа инструмента по задней поверхности или нормально к обработанной поверхности) и силой трения Т, действующей по задней поверхности.
 

Индуктивное сопротивление в аэродинамике

Индуктивное сопротивление (англ. lift-induced drag) — это следствие образования подъёмной силы на крыле конечного размаха. Несимметричное обтекание крыла приводит к тому, что поток воздуха сбегает с крыла под углом к набегающему на крыло потоку (т. н. скос потока). Таким образом, во время движения крыла происходит постоянное ускорение массы набегающего воздуха в направлении, перпендикулярном направлению полёта, и направленном вниз. Это ускорение, во-первых, сопровождается образованием подъёмной силы, а во-вторых — приводит к необходимости сообщать ускоряющемуся потоку кинетическую энергию. Количество кинетической энергии, необходимое для сообщения потоку скорости, перпендикулярной направлению полёта, и будет определять величину индуктивного сопротивления.

На величину индуктивного сопротивления оказывает влияние не только величина подъёмной силы, но и её распределение по размаху крыла. Минимальное значение индуктивного сопротивления достигается при эллиптическом распределении подъёмной силы по размаху.
При проектировании крыла этого добиваются следующими методами:

• выбором рациональной формы крыла в плане;
• применением геометрической и аэродинамической крутки;
• установкой вспомогательных поверхностей — вертикальных законцовок крыла.

Индуктивное сопротивление пропорционально квадрату подъёмной силы Y, и обратно пропорционально площади крыла S, его удлинению λ{\displaystyle \lambda }, плотности среды ρ и квадрату скорости V:

Xi=CxiρV22S=Cy2πλρV22S=1πλY2ρV22S{\displaystyle X_{i}=C_{xi}{\frac {\rho V^{2}}{2}}S={\frac {C_{y}^{2}}{\pi \lambda }}{\frac {\rho V^{2}}{2}}S={\frac {1}{\pi \lambda }}{\frac {Y^{2}}{{\frac {\rho V^{2}}{2}}S}}}

Таким образом, индуктивное сопротивление вносит существенный вклад при полёте на малой скорости (и, как следствие, на больших углах атаки). Оно также увеличивается при увеличении веса самолёта.

ФИЗИКА

§ 3.15. Сила сопротивления при движении тел в жидкостях и газах

При движении твердого тела в жидкости или газе или при движении одного слоя жидкости (газа) относительно другого тоже возникает сила, тормозящая движение, — сила жидкого трения или сила сопротивления.

Сила сопротивления направлена параллельно поверхности соприкосновения твердого тела с жидкостью (газом) в сторону, противоположную скорости тела относительно среды, и тормозит движение(1).

Сила сопротивления (жидкого трения) обычно значительно меньше силы сухого трения. Именно поэтому для уменьшения сил трения между движущимися деталями машин применяют смазку.

Главная особенность силы сопротивления состоит в том, что она появляется только при относительном движении тела и окружающей среды. Сила трения покоя в жидкостях и газах полностью отсутствует. Это приводит к тому, что усилием рук можно сдвинуть тяжелое тело, например баржу, в то время как сдвинуть с места, скажем, гусеничный трактор усилием рук просто невозможно.

Убедитесь в том, что плавающий деревянный брусок сразу же придет в движение, если на него слегка подуть. Попробуйте проделать то же самое с бруском, лежащим на столе.

Модуль силы сопротивления _c зависит от размеров, формы и состояния поверхности тела, свойств (вязкости) среды (жидкости или газа), в которой движется тело, и, наконец, от относительной скорости движения тела и среды.

Для того чтобы уменьшить силу сопротивления среды, телу придают обтекаемую форму. Наиболее выгодна в этом отношении сигарообразная форма (рис. 3.40), близкая к форме падающей капли дождя или рыбы.

Рис. 3.40

Влияние формы тела на силу сопротивления наглядно показано на рисунке 3.41. Модуль силы сопротивления цилиндра обозначим через . Конусообразная насадка к цилиндру уменьшает силу сопротивления от 1/2 до 1/4 в зависимости от размера угла при вершине конуса. Сглаженная насадка доводит силу сопротивления до 1/5. Наконец, если придать телу сигарообразную форму, то при том же поперечном сечении сила сопротивления уменьшается до 1/25. По сравнению с телом сигарообразной формы сила сопротивления для шара (имеющего такую же площадь поперечного сечения) больше в несколько раз, а для тонкого диска, плоскость которого перпендикулярна направлению скорости, — в несколько десятков раз. Особенно велика сила сопротивления, возникающая при движении полусферы вогнутой стороной вперед. По этой причине парашюты имеют часто форму полусферы.

Рис. 3.41

Примерный характер зависимости модуля силы сопротивления от модуля относительной скорости тела приведен на рисунке 3.42. Если тело неподвижно относительно вязкой среды (относительная скорость равна нулю), то сила сопротивления равна нулю. С увеличением относительной скорости сила сопротивления растет медленно, а потом все быстрее и быстрее.

Рис. 3.42

При малых скоростях движения в жидкости (газе) силу сопротивления можно считать приближенно прямо пропорциональной скорости движения тела относительно среды:

где k₁ — коэффициент сопротивления, зависящий от формы, размеров, состояния поверхности тела и свойств среды — ее вязкости. Коэффициент k₂ в СИ выражается в Н • с/м = кг/с. Его значение определяют опытным путем.

При больших скоростях относительного движения сила сопротивления пропорциональна квадрату скорости:

где коэффициент сопротивления k₂ выражается в Н • с2/м2 = = кг/м.

Какую именно формулу следует применять в данном конкретном случае, устанавливают опытным путем. При падении тел в воздухе сила сопротивления становится пропорциональной квадрату скорости практически с самого начала падения.

При ускоренном движении тела в жидкости для учета воздействия жидкости на это тело надо к массе тела прибавить так называемую присоединенную массу. Присоединенная масса зависит от формы тела и плотности среды. В дальнейшем при решении задач присоединенную массу мы учитывать не будем.

Жидкое трение возникает между поверхностью твердого тела и окружающей его жидкой или газообразной средой, в которой оно движется. При медленном движении сила сопротивления пропорциональна скорости, а при быстром — квадрату скорости.

(1) Впрочем, движущийся поток воды или воздуха может увлекать за собой тело. Например, когда ветер гонит опавшие листья, то сила трения со стороны воздуха направлена по движению листьев. Но и в этом случае она противоположна скорости движения тела (листьев) относительно среды (воздуха). В приведенном примере воздух и листья, хотя и движутся в одном направлении, но скорость воздуха больше, листья отстают от ветра.

Проект «Приводные парашюты. Альтернативные способы использования парашютов»

Полет
на парашюте с двигателем лучше всего
можно описать как картинг в воздухе.
Звучит круто? Но такая конструкция –
это не просто захватывающий способ
увидеть мир. У них есть и другие важные
сферы применения. В проекте исследуются
возможности применения этого экологически
чистого, относительно безопасного и
чрезвычайно приятного вида транспорта.

В
этом проекте рассматривается концепция
парашютов с электроприводом как
транспорта будущего.

Цели
проекта:

Что нам понадобится:

• компьютер с доступом в интернет;
• цифровая камера;
• типичные канцтовары / товары для рукоделия (например, бумага, ручки и картон);
• маленький мотор (спросите в хозяйственном магазине или в магазине поделок);

Ход эксперимента:

1. Если речь идет о парашюте с электроприводом, необходимо соблюдать меры безопасности.
2. Прочитайте материалы на соответствующие темы.
3. Изучите основную конструкцию парашюта с двигателем с помощью онлайн-поиска и (если возможно) посетите аэродромы, где взлетают парапланы.
4. Спроектируйте и постройте свою небольшую модель. Если возможно, улучшите существующую конструкцию.
5. Опишите свой метод в подробном отчете.
6. Покажите свои рабочие модели на научной ярмарке.
7. Возьмите с собой любые интересные фотографии, сделанные на протяжении всего эксперимента.

Вывод:

Что
именно представляет собой парашют с
двигателем? Каковы важные современные
способы использования такой конструкции
с электроприводом? Каковы возможные
варианты использования такого
парашюта в будущем? Почему на данный
момент он не получил широкое распространение?
Как можно улучшить это изобретение для
более широкого использования?

Расчет сил сопротивления

Фильтр нулевого сопротивления плюсы и минусы. Неудобная правда С целью определения сил сопротивления потребуется применение третьего закона Ньютона. Такая величина, как сила сопротивления, будет численно равной силе, которую потребуется приложить с целью равномерного движения предмета по горизонтальной ровной поверхности. Это становится возможным с помощью динамометра.

Таким образом, искомая величина оказывается прямо пропорциональной массе тела

Стоит при этом учитывать во внимание, что для более точного подсчета потребуется выбрать $u$ коэффициент, зависимый от материала изготовления опоры. Также принимается во внимание материал изготовления самого предмета исследования. При расчете применяется постоянная $g$, чье значение 9,8 $м/с^2$

При расчете применяется постоянная $g$, чье значение 9,8 $м/с^2$.

В условиях движения тела на высоте, на него влияет сила трения воздуха, зависимая от скорости перемещения предмета. Искомую величину определяют на основании такой формулы (подходящей исключительно для тел с передвижением с небольшой скоростью):

$F = va$, где:

• $v$ – скорость движения предмета,
• $a$ – коэффициент сопротивления среды.

Движение тела, брошенного под углом к горизонту

С задачей о свободном падении тела тесно связана задача о движении тела, брошенного под определенным углом к горизонту. Так, движение по параболической траектории можно представить как сумму двух независимых движений относительно вертикальной и горизонтальной осей.

Вдоль оси OY тело движется равноускоренно с ускорением g, начальная скорость этого движения — vy. Движение вдоль оси OX — равномерное и прямолинейное, с начальной скоростью vx.

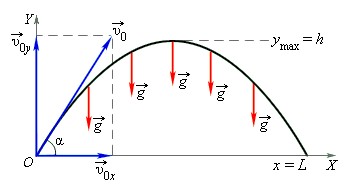
Условия для движения вдоль оси ОХ:

x=; vx=vcosα; ax=.

Условия для движения вдоль оси OY:

y=; vy=vsinα; ay=-g.

Приведем формулы для движения тела, брошенного под углом к горизонту.

Время полета тела:

t=2vsinαg.

Дальность полета тела:

L=v2sin2αg.

Максимальная дальность полета достигается при угле α=45°.

Lmax=v2g.

Максимальная высота подъема:

h=v2sin2α2g.

Отметим, что в реальных условиях движение тела, брошенного под углом к горизонту, может проходить по траектории, отличной от параболической вследствие сопротивления воздуха и ветра. Изучением движения тел, брошенных в пространстве, занимается специальная наука — баллистика.

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Индуктивное сопротивление в аэродинамике

Индуктивное сопротивление (англ. lift-induced drag) — это следствие образования подъёмной силы на крыле конечного размаха. Несимметричное обтекание крыла приводит к тому, что поток воздуха сбегает с крыла под углом к набегающему на крыло потоку (т. н. скос потока). Таким образом, во время движения крыла происходит постоянное ускорение массы набегающего воздуха в направлении, перпендикулярном направлению полёта, и направленном вниз. Это ускорение, во-первых, сопровождается образованием подъёмной силы, а во-вторых — приводит к необходимости сообщать ускоряющемуся потоку кинетическую энергию. Количество кинетической энергии, необходимое для сообщения потоку скорости, перпендикулярной направлению полёта, и будет определять величину индуктивного сопротивления.

На величину индуктивного сопротивления оказывает влияние не только величина подъёмной силы, но и её распределение по размаху крыла. Минимальное значение индуктивного сопротивления достигается при эллиптическом распределении подъёмной силы по размаху.
При проектировании крыла этого добиваются следующими методами:

• выбором рациональной формы крыла в плане;
• применением геометрической и аэродинамической крутки;
• установкой вспомогательных поверхностей — вертикальных законцовок крыла.

Индуктивное сопротивление пропорционально квадрату подъёмной силы Y, и обратно пропорционально площади крыла S, его удлинению λ{\displaystyle \lambda }, плотности среды ρ и квадрату скорости V:

Xi=CxiρV22S=Cy2πλρV22S=1πλY2ρV22S{\displaystyle X_{i}=C_{xi}{\frac {\rho V^{2}}{2}}S={\frac {C_{y}^{2}}{\pi \lambda }}{\frac {\rho V^{2}}{2}}S={\frac {1}{\pi \lambda }}{\frac {Y^{2}}{{\frac {\rho V^{2}}{2}}S}}}

Таким образом, индуктивное сопротивление вносит существенный вклад при полёте на малой скорости (и, как следствие, на больших углах атаки). Оно также увеличивается при увеличении веса самолёта.