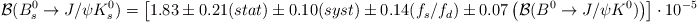Метрология, стандартизация и сертификация

Введение

Все, что сказано в этом введении, запоминать не нужно. это справочный материал, к которому вы будете обращаться при выполнении лабораторных работ.

1. Как определять погрешности измерений

Выполнение лабораторных работ связано с измерением различных физических величин и последующей обработкой их результатов.

Измерение — нахождение значения физической величины опытным путем с помощью средств измерений.

Прямое измерение — определение значения физической величины непосредственно средствами измерения.

Косвенное измерение — определение значения физической величины по формуле, связывающей ее с другими физическими величинами, определяемыми прямыми измерениями.

Введем следующие обозначения:

A, B, C, … — физические величины.

A_пр — приближенное значение физической величины, т.е. значение, полученное путем прямых или косвенных измерений.

ΔA — абсолютная погрешность измерения физической величины.

ε — относительная погрешность измерения физической величины, равная:

Δ_иA — абсолютная инструментальная погрешность, определяемая конструкцией прибора (погрешность средств измерения; указывается в каждой работе при описании прибора в разделе Оборудование и средства измерения)

Δ_оA — абсолютная погрешность отсчета (получающаяся от недостаточно точного отсчета показаний средств измерения), она равна в большинстве случаев половине цены деления; при измерении времени — цене деления секундомера или часов.

Максимальная абсолютная погрешность прямых измерений складывается из абсолютной инструментальной погрешности и абсолютной погрешности отсчета при отсутствии других погрешностей:

ΔA=Δ_иA + Δ_оA

Абсолютную погрешность измерения обычно округляют до одной значащей цифры (ΔA≈0,17=0,2); численное значение результата измерений округляют так, чтобы его последняя цифра оказалась в том же разряде, что и цифра погрешности (А=10,332≈10,3).

Результаты повторных измерений физической величины А, проведенных при одних и тех же контролируемых условиях и при использовании достаточно чувствительных и точных (с малыми погрешностями) средств измерения, отличаются друг от друга.

В этом случае A_пр находят как среднее арифметическое значение всех измерений, а ΔA (ее в этом случае называют случайной погрешностью) определяют методами математической статистики.

В школьной лабораторной практике такие средства измерения практически не используются. Поэтому при выполнении лабораторных работ необходимо определять максимальные погрешности измерения физических величин. При этом для получения результата достаточно одного измерения.

Относительная погрешность косвенных измерений определяется, как показано в таблице 1.

Абсолютная погрешность косвенных измерений определяется по формуле ΔA=A_прε (ε выражается десятичной дробью).

Таблица 1

Формулы для нахождения относительной погрешности косвенных измерений

Nº п/п	Формула физической величины	Формула относительной погрешности
1
2
3	A=B+C
4

2. О классе точности электроизмерительных приборов

Для определения абсолютной инструментальной погрешности прибора надо знать его класс точности. Класс точности γ_пр измерительного прибора показывает, сколько процентов составляет абсолютная инструментальная погрешность Δ_иA от всей шкалы прибора (A_max):

Класс точности указывается при описании прибора в разделе Оборудование и средства измерения. Cуществуют следующие классы точности электроизмерительных приборов: 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Зная класс точности прибора (γ_пр) и всю его шкалу (A_max), определяют абсолютную погрешность Δ_иA измерения физической величины А этим прибором:

3. Как сравнивать результаты измерений

1. Записать результаты измерений в виде двойных неравенств:

A_{1 пр} – ΔA₁ < A_{1 пр} < A_{1 пр} + ΔA₁
A_{2 пр} – ΔA₂ < A_{2 пр} < A_{2 пр} + ΔA₂
2. Сравнить полученные интервалы значений (рис.1): если интервалы не перекрываются, то результаты неодинаковы, если перекрываются — одинаковы при данной относительной погрешности измерений.

Рисунок 1.

4. Как оформлять отчет о проделанной работе

Отчетом о проделанной работе является форма, находящаяся в левом нижнем окне. После ее заполнения надо нажать на кнопку «Отправить результаты на сервер».

Значения измеренных физических величин переносятся в таблицу результатов автоматически после нажатия соответствующей кнопки.

Значения остальных величин и ответ на контрольный вопрос вводятся с клавиатуры.

домашней странице BARSIC

Погрешности измерений, представление результатов эксперимента

п.1. Шкала измерительного прибора

Примеры шкал различных приборов:

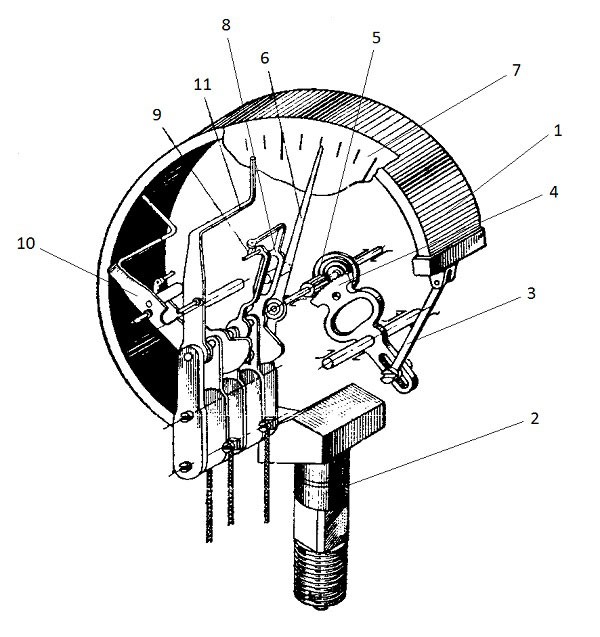
Манометр – прибор для измерения давления, круговая шкала

Вольтметр – прибор для измерения напряжения, дуговая шкала

Индикатор громкости звука, линейная шкала

п.2. Цена деления

Пример определения цены деления:

Определим цену деления основной шкалы секундомера.Два ближайших пронумерованных деления на основной шкале: a = 5 cb = 10 c Между ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления.

Цена деления: \begin \triangle=\frac\\ \triangle=\frac=\frac15=0,2\ c \end

Погрешность измерения и принцип неопределенности Гейзенберга

Принцип неопределенности Гейзенберга устанавливает предел точности одновременного определения пары наблюдаемых физических величин, характеризующих квантовую систему, описываемых некоммутирующими операторами (например, координаты и импульса, тока и напряжения, электрического и магнитного поля). Таким образом, из аксиом квантовой механики следует принципиальная невозможность одновременного определения с абсолютной точностью некоторых физических величин. Этот факт накладывает серьёзные ограничения на применимость понятия «истинное значение физической величины»[источник не указан 233 дня].

Учимся определять погрешность взвешивания

Это один из примеров прямых измерений. На особом месте стоит взвешивание. Ведь у рычажных весов нет шкалы. Научимся определять погрешность такого процесса. На точность измерения массы влияет точность гирь и совершенство самих весов.

Мы пользуемся рычажными весами с набором гирь, которые необходимо класть именно на правую чашу весов. Для взвешивания возьмем линейку.

Перед началом опыта нужно уравновесить весы. Линейку кладем на левую чашу.

Масса будет равна сумме установленных гирь. Определим погрешность измерения этой величины.

D m = D m (весов) + D m (гирь)

Погрешность измерения массы складывается из двух слагаемых, связанных с весами и гирями. Чтобы узнать каждую из этих величин, на заводах по выпуску весов и гирь продукция снабжается специальными документами, которые позволяют вычислить точность.

Абсолютная и относительная погрешность

Абсолютной погрешностью или, короче, погрешностью приближенного
числа называется разность между этим числом и его точным значением (из большего числа вычитается меньшее)*.

Пример 1. На предприятии 1284 рабочих и служащих. При
округлении этого числа до 1300 абсолютная погрешность
составляет 1300 — 1284 = 16. При округлении до 1280 абсолютная погрешность составляет 1284 — 1280 = 4.

Относительной погрешностью приближенного числа называется отношение
абсолютной погрешности приближенного числа к самому этому числу.

Пример 2. В школе 197 учащихся. Округляем это число до 200. Абсолютная
погрешность составляет 200 — 197 = 3. Относительная погрешность равна 3/197 или, округленно, 3/197 = 1,5 %.

В большинстве случаев невозможно узнать точное значение приближенного числа, а значит, и точную величину погрешности.
Однако почти всегда можно установить, что погрешность (абсолютная или относительная) не превосходит некоторого числа.

Пример 3. Продавец взвешивает арбуз на чашечных весах. В наборе гирь наименьшая — 50 г. Взвешивание дало 3600 г. Это число – приближенное. Точный вес арбуза
неизвестен. Но абсолютная погрешность не
превышает 50 г. Относительная погрешность не превосходит 50/3600 ≈ 1,4%.

Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей), называется предельной абсолютной погрешностью. Число, заведомо превышающее
относительную погрешность (или в худшем случае равное ей), называется предельной относительной погрешностью.

В примере 3 за предельную абсолютную погрешность можно взять 50 г, а за предельную относительную погрешность — 1,4 %.

Величина предельной погрешности не является вполне определенной. Так, в примере 3 можно принять за предельную абсолютную
погрешность 100 г, 150 г и вообще всякое число, большее чем 50 г. На практике берется по возможности меньшее значение
предельной погрешности. В тех случаях, когда известна точная величина погрешности, эта величина служит одновременно
предельной погрешностью. Для каждого приближенного числа должна быть известна его предельная погрешность
(абсолютная или oотносительная). Когда она прямо не указана, подразумевается что предельная абсолютная погрешность
составляет половину единицы последнего выписанного разряда. Так, если приведено приближенное число 4,78 без указания
предельной погрешности, то подразумевается, что предельная абсолютная погрешность составляет 0,005. Вследствие этого
соглашения всегда можно обойтись без указания предельной погрешности числа.

Предельная абсолютная погрешность обозначается греческой буквой Δ («дельта»); предельная относительная
погрешность — греческой буквой δ («дельта малая»). Если приближенное число обозначить буквой а, то

δ = Δ/a.

Пример 4. Длина карандаша измерена линейкой с миллиметровыми делениями. Измерение показало 17,9 см. Какова предельная
относительная погрешность этого измерения?
Здесь а = 17,9 см; можно принять Δ = 0,1 см, так как с точностью до 1 мм измерить карандаш нетрудно, a значительно уменьшить, предельную погрешность ни удастся (при навыке можно прочесть на хорошей линейке и 0,02 и даже 0,01 см, но у самого карандаша ребра могут разниться на бoльшую величину). Относительная погрешность равна 0,1/17,9.
Округляя, находим δ = 0,1/18 ≈ 0,6%.

Пример 5. Цилиндрический поршень имеет около 35 мм в диаметре. С какой точностью нужно его измерить микрометром, чтобы
предельная относительная погрешность составляла 0,05%?Решение. По условию, предельная абсолютная погрешность должна составлять 0,05% от 35 мм. Следовательно, предельная
абсолютная погрешность равна 36*(0,05/100) = 0,0175 (мм) или, усиливая, 0,02 (мм). Можно воспользоваться
формулой δ = Δ/a.
Подставляя в неё а = 35, δ = 0,0005, имеем 0,0005 = Δ/35. Значит, Δ = 35 • 0,0005 = 0,0175 (мм).

* Иначе говоря, если a есть приближенное число, а х – его точное значение, то абсолютная погрешность есть абсолютное
значение разности a – х. В некоторых руководствах абсолютной погрешностью называется сама
разность a – х (или разность х — a). Эта величина может быть положительной или отрицательной.

Классификация погрешностей измерений

По способу выражения

Абсолютная погрешность

Абсолютной называют погрешность, выраженную в единицах измеряемой величины. Её можно описать формулой ΔX=Xизм−Xист.{\displaystyle \Delta X=X_{\text{изм}}-X_{\text{ист}}.} Вместо истинного значения измеряемой величины, на практике пользуются действительным значением Xд,{\displaystyle {X_{\text{д}}},} которое достаточно близко к истинному, определяется экспериментальным путем и в конкретной задаче может приниматься вместо него. Из-за того что истинное значение величины всегда неизвестно, можно лишь оценить границы, в которых лежит погрешность, с некоторой вероятностью. Такая оценка выполняется методами математической статистики.

Относительная погрешность

Относительная погрешность выражается отношением δX=ΔXXд.{\displaystyle \delta X={\frac {\Delta X}{X_{\text{д}}}}.} Относительная погрешность является безразмерной величиной; её численное значение может указываться, например, в процентах.

По источнику возникновения

Инструментальная погрешность

Эта погрешность определяется несовершенством прибора, возникающим, например, вследствие расхождения его реальной функции преобразования от калибровочной зависимости.

Методическая погрешность

Методической называют погрешность, обусловленную несовершенством метода измерений. К таким можно отнести погрешности от неадекватности принятой модели объекта от реального объекта или от неточности расчётных формул.

Субъективная погрешность

Субъективной является погрешность, обусловленная ограничениями человека, как оператора при проведении измерений. Проявляется, например, в неточностях при отсчете показаний со шкалы прибора.

По характеру проявления

Случайная погрешность

Это составляющая погрешности измерения, изменяющаяся случайным образом в серии повторных измерений одной и той же величины, проведенных в одних и тех же условиях. В появлении таких погрешностей не наблюдается какой-либо закономерности, они обнаруживаются при повторных измерениях одной и той же величины в виде некоторого разброса получаемых результатов. Случайные погрешности неизбежны, неустранимы и всегда присутствуют в результате измерения, однако их влияние обычно можно устранить статистической обработкой. Описание случайных погрешностей возможно только на основе теории случайных процессов и математической статистики.

Математически случайную погрешность, как правило, можно представить белым шумом: как непрерывную случайную величину, симметричную относительно нуля, независимо реализующуюся в каждом измерении (некоррелированную по времени).

Основным свойством случайной погрешности является возможность уменьшения искажения искомой величины путём усреднения данных. Уточнение оценки искомой величины при увеличении количества измерений (повторных экспериментов) означает, что среднее случайной погрешности при увеличении объёма данных стремится к 0 (закон больших чисел).

Часто случайные погрешности возникают из-за одновременного действия многих независимых причин, каждая из которых в отдельности слабо влияет на результат измерения. По этой причине часто полагают распределение случайной погрешности «нормальным» (см. Центральная предельная теорема). «Нормальность» позволяет использовать в обработке данных весь арсенал математической статистики.

Однако априорная убежденность в «нормальности» на основании Центральной предельной теоремы не согласуется с практикой — законы распределения ошибок измерений весьма разнообразны и, как правило, сильно отличаются от нормального.

Случайные погрешности могут быть связаны с несовершенством приборов (трение в механических приборах и т. п.), тряской в городских условиях, с несовершенством объекта измерений (например, при измерении диаметра тонкой проволоки, которая может иметь не совсем круглое сечение в результате несовершенства процесса изготовления).

Систематическая погрешность

Это погрешность, изменяющаяся во времени по определённому закону (частным случаем является постоянная погрешность, не изменяющаяся с течением времени). Систематические погрешности могут быть связаны с ошибками приборов (неправильная шкала, калибровка и т. п.), неучтёнными экспериментатором.

Систематическую ошибку нельзя устранить повторными измерениями. Её устраняют либо с помощью поправок, либо «улучшением» эксперимента.

Деление погрешностей на случайные и систематические достаточно условно. Например, ошибка округления при определённых условиях может носить характер как случайной, так и систематической ошибки.

ВЕСА РЕЗУЛЬТАТОВ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ

При неравноточных измерениях, когда результаты каждого измерения нельзя считать одинаково надежными, уже нельзя обойтись определением простого арифметического среднего. В таких случаях учитывают достоинство (или надежность) каждого результата измерений.Достоинство результатов измерений выражают некоторым числом, называемым весом этого измерения. Очевидно, что арифметическое среднее будет иметь больший вес по сравнению с единичным измерением, а измерения, выполненные при использовании более совершенного и точного прибора, будут иметь большую степень доверия, чем те же измерения, выполненные прибором менее точным.
Поскольку условия измерений определяют различную величину средней квадратической погрешности, то последнюю и принято принимать в качестве основы оценки весовых значений, проводимых измерений. При этом веса результатов измерений принимают обратно пропорциональными квадратам соответствующих им средних квадратических погрешностей.
Так, если обозначить через р и Р веса измерений, имеющие средние квадратические погрешности соответственно m и µ, то можно записать соотношение пропорциональности:

Например, если µ средняя квадратическая погрешность арифметического среднего, а m – соответственно, одного измерения, то, как следует из

можно записать:

т. е. вес арифметического среднего в n раз больше веса единичного измерения.

Аналогичным образом можно установить, что вес углового измерения, выполненного 15-секундным теодолитом, в четыре раза выше веса углового измерения, выполненного 30-секундным прибором.

При практических вычислениях обычно вес одной какой-либо величины принимают за единицу и при этом условии вычисляют веса остальных измерений. Так, в последнем примере если принять вес результата углового измерения 30-секундным теодолитом за р = 1, то весовое значение результата измерения 15-секундным теодолитом составит Р = 4.

§ 5. Точность и погрешность измерений

Всякое измерение может быть выполнено с большей или меньшей точностью.

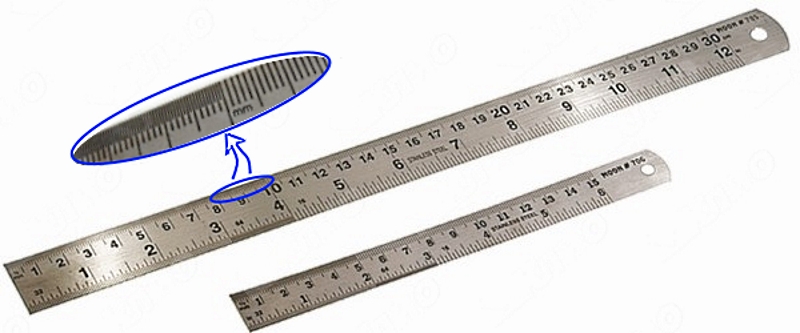
В качестве примера рассмотрим измерение длины ручки демонстрационным метром с сантиметровыми делениями (рис. 14).

Вначале определим цену деления линейки. Она будет равна 1 см.

Если верхний конец ручки совместить с нулевым штрихом, то нижний будет находиться между 11 и 12 штрихами, но ближе к 11.

Какое же из этих двух значений следует принять за длину ручки? Очевидно, то, которое ближе к истинному значению, т. е. 11 см.

Считая, что длина ручки 11 см, мы допустили неточность, так как ручка чуть длиннее 11 см.

В физике допускаемую при измерении неточность называют погрешностью измерений.

Погрешность измерения не может быть больше цены деления шкалы измерительного прибора.

В нашем случае погрешность измерения ручки не превышает 1 см. Если такая точность измерений нас не удовлетворяет, то можно произвести измерения с большей точностью. Но тогда придётся взять масштабную линейку с миллиметровыми делениями, т. е. с ценой деления 1 мм.

В этом случае длина ручки окажется равной 11,2 см.

Из этого примера видно, что точность измерений зависит от цены деления шкалы прибора.

Чем меньше цена деления, тем больше точность измерения.

Точность измерения зависит также от правильного применения измерительного прибора, расположения глаза при отсчёте по прибору.

Вследствие несовершенства измерительных приборов и наших органов чувств при любом измерении получаются лишь приближённые значения, несколько большие или меньшие истинного значения измеряемой величины.

Во время выполнения лабораторных работ или просто измерений следует считать, что погрешность измерений равна половине цены деления шкалы измерительного прибора.

Измерим длину карандаша. Нулевую отметку линейки совместим с одним концом карандаша, а другой её конец окажется вблизи 14 см. Цена деления линейки 1 мм, тогда погрешность измерения будет равна 0,5 мм или 0,05 см.

Следовательно, длину карандаша можно записать в виде

где I — длина карандаша.

Истинное значение длины карандаша находится в интервале от 13,95 см до 14,05 см.

При записи величин, с учётом погрешности, следует пользоваться формулой

где А — измеряемая величина, а — результат измерений, Δа — погрешность измерений (Δ — греч. буква «дельта»).

Как определять погрешность измерений (учебник Физика 10)

1. Как определять погрешности измерений.

Выполнение лабораторных работ связано с измерением различных физических величин и последующей обработкой их результатов.

Измерение — нахождение значения физической величины опытным путем с помощью средств измерений.

Прямое измерение — определение значения физической величины непосредственно средствами измерения.

Косвенное измерение — определение значения физической величины по формуле, связывающей ее с другими физическими величинами, определяемыми прямыми измерениями.

Введем следующие обозначения:

А, В, С, . — физические величины.

А_пр — приближенное значение физической величины, т. е. значение, полученное путем прямых или косвенных измерений.

ΔА — абсолютная погрешность измерения физической величины.

ε — относительная погрешность измерения физической величины, равная:

Δ_ИА — абсолютная инструментальная погрешность, определяемая конструкцией прибора (погрешность средств измерения; см. табл. 1).

ΔА — абсолютная погрешность отсчета (получающаяся от недостаточно точного отсчета показаний средств измерения); она равна в большинстве случаев половине цены деления, при измерении времени — цене деления секундомера или часов.

Абсолютные инструментальные погрешности средств измерений

№	Средства измерения	Предел измерения	Цена деления	Абсолютная инструментальная погрешность
1	Линейка
ученическая	до 50 см	1 мм	± 1 мм
чертежная	до 50 см	1 мм	± 0,2 мм
инструментальная (стальная)	20 см	1 мм	± 0,1 мм
демонстрационная	100 см	1 см	± 0,5 см
2	Лента измерительная	150 см	0,5 см	± 0,5 см
3	Измерительный цилиндр	до 250 мл	1 мл	± 1 мл
4	Штангенциркуль	150 мм	0,1 мм	± 0,05 мм
5	Микрометр	25 мм	0,01 мм	± 0,005 мм
6	Динамометр учебный	4 Н	0,1 Н	± 0,05 Н
7	Весы учебные	200 г	—	± 0,01 г
8	Секундомер	0-30 мин	0,2 с	± 1 с за 30 мин
9	Барометр-анероид	720-780 мм рт. ст.	1 мм рт. ст.	± 3 мм рт. ст.
10	Термометр лабораторный	0-100 0 С	1 0 С	± 1 0 С
11	Амперметр школьный	2 А	0,1 А	± 0,05 А
12	Вольтметр школьный	6 В	0,2 В	± 0,15 В

Максимальная абсолютная погрешность прямых измерений складывается из абсолютной инструментальной погрешности и абсолютной погрешности отсчета при отсутствии других погрешностей:

Абсолютную погрешность измерения обычно округляют до одной значащей цифры (ΔА = 0,17 ≈ 0,2); числовое значение результата измерений округляют так, чтобы его последняя цифра оказалась в том же разряде, что и цифра погрешности (А = 10,332 ≈ 10,3).

Результаты повторных измерений физической величины А, проведенных при одних и тех же контролируемых условиях и при использовании достаточно чувствительных и точных (с малыми погрешностями) средств измерения, обычно отличаются друг от друга. В этом случае А_пр находят как среднее арифметическое значение всех измерений, а погрешность ΔА (ее называют случайной погрешностью) определяют методами математической статистики.

В школьной лабораторной практике такие средства измерения практически не используются. Поэтому при выполнении лабораторных работ необходимо определять максимальные погрешности измерения физических величин. Для получения результата достаточно одного измерения.

Относительная погрешность косвенных измерений определяется так, как показано в таблице 2.

Формулы для вычисления относительной погрешности косвенных измерений

№	Формула для физической величины	Формула для относительной погрешности
1
2
3
4

Абсолютная погрешность косвенных измерений определяется по формуле ΔА = А_прε (ε выражается десятичной дробью).

2. О классе точности электроизмерительных приборов.

Для определения абсолютной инструментальной погрешности прибора надо знать его класс точности. Класс точности γ_пр измерительного прибора показывает, сколько процентов составляет абсолютная инструментальная погрешность Δ_иА от всей шкалы прибора (A_max):

Класс точности указывают на шкале прибора или в его паспорте (знак % при этом не пишут). Существуют следующие классы точности электроизмерительных приборов: 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Зная класс точности прибора (γ_пр) и всю его шкалу (А_mах), определяют абсолютную погрешность Δ_иА измерения физической величины А этим прибором:

3. Как сравнивать результаты измерений.

1. Записать результаты измерений в виде двойных неравенств:

Источник

Абсолютная погрешность — измерительный прибор

Абсолютная погрешность измерительного прибора представляет собой расхождение ( разность) между измеренным Ли и действительным ( истинным) Лд значениями измеряемой величины ДЛ — / 4н — Ац. Истинное значение измеряемой величины находят с учетом поправки. Поправка — это величина, обратная по знаку абсолютной погрешности: ДР — ДЛ Ал-А. Абсолютная погрешность электроизмерительных приборов со стрелочным показателем практически неизменна в пределах всей шкалы, поэтому с уменьшением значения измеряемой величины она возрастает. Для повышения точности измерения измеряемой величины на показывающих приборах со стрелочным указателем следует выбирать такие пределы измерения, чтобы отсчитывать показания примерно в пределах 2 / 3 всей шкалы.
 

Абсолютная погрешность измерительного прибора равна разности между показанием прибора и действительным ( точным) значением измеряемой величины.
 

Абсолютная погрешность измерительного прибора определяется разностью между показанием прибора и истинным значением измеряемой величины. Погрешность показаний прибора имеет своими источниками погрешности отдельных его элементов: чувствительного элемента, передаточного механизма и шкалы. Погрешность чувствительного элемента заключается в том, что действительная зависимость его перемещений от измеряемой величины не совпадает с расчетной, заложенной в схему прибора. Погрешность шкалы складывается из ошибки положения ее штрихов и эксцентриситета шкалы.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины. Так как истинное значение измеряемой величины установить нельзя, в измерительной технике используется так называемое действительное значение, полученное с помощью образцового прибора.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины. Поскольку последнее установить нельзя, то в измерительной технике используют так называемое действительное значение, полученное посредством образцового прибора.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины Так как величину истинного значения измеряемой величины установить нельзя, в измерительной технике используется так называемое действительное значение, полученное с помощью образцового прибора.
 

Приведенная погрешность измерительного прибора — отношение абсолютной погрешности измерительного прибора к нормирующему значению, выраженное в процентах.
 

Корректность поставленных экспериментов доказана отсутствием превышения абсолютных ошибок измерения как при определении перемещений, так и напряжений над абсолютной погрешностью используемых измерительных приборов.
 

В некоторых случаях ( для образцовых и рабочих средств измерений повышенной точности) для исключения систематической погрешности показаний вводят поправку, равную абсолютной погрешности измерительного прибора.
 

Абсолютная погрешность измерительного прибора определяется разностью между показанием прибора и действительным значением измеряемой величины.
 

В данном разделе будут рассмотрены виды погрешностей, свойственные мерам, отдельным элементам и устройствам, а также средствам измерений в целом. Под абсолютной погрешностью меры понимают разность ( отклонение от номинального значения) между номинальным значением меры и истинным значением воспроизводимой ею величины. Так как истинное значение величины остается неизвестным, то на практике вместо него используют действительное значение величины. Следует различать абсолютную погрешность измерительного преобразователя по входу и по выходу. Абсолютную погрешность измерительного преобразователя по входу находят как разность между значением величины на входе преобразователя, определяемой в принципе по истинному значению величины на его выходе с помощью градуировочной характеристики, приписанной преобразователю, и истинным значением величины на входе преобразователя. Абсолютную погрешность измерительного преобразователя по выходу находят как разность между истинным значением величины на выходе преобразователя, отображающей измеряемую величину, и значением величины на выходе, определяемой в принципе по истинному значению величины на выходе с помощью градуировочной характеристики, приписанной преобразователю. Относительная погрешность измерительного прибора определяется как отношение абсолютной погрешности измерительного прибора к истинному значению измеряемой им величины.