Формула расчета мощности по току и напряжению электросхемы

Содержание:

Мощность
- Еще одна формула для расчета мощности
Основные параметры электродвигателя
Нужны ли устройства компенсации в быту?
Мощность вращающихся объектов
Работа — разность кинетической энергии
Определение и формулы мощности
Знак работы силы
Определение мощности электродвигателя по потребляемому току
Часто задаваемые вопросы
Примеры решения задач
Мощность электрического тока
Мощность
- Еще одна формула для расчета мощности

Мощность

В механике мощность часто обозначают символами N или P и измеряют в Ваттах в честь шотландского изобретателя Джеймса Уатта.

Примечание: Символ $\vec$ используется для обозначения силы реакции опоры — она измеряется в Ньютонах и является векторной величиной. Чтобы не возникло путаницы, мощность вместо N будем обозначать символом P. Символ P – первая буква в английском слове power – мощность.

Мощность – это работа, совершенная за одну секунду (энергия, затраченная за 1 сек).

Расчет работы осуществляем, используя любую из формул:

\[ \large A = \Delta E_

Разделив эту работу на время, в течение которого она совершалась, получим мощность.

Если работа совершалась равными частями за одинаковые интервалы времени – мощность будет постоянной величиной.

Мощность переменная, когда в некоторые интервалы времени совершалось больше работы.

Еще одна формула для расчета мощности

Есть еще один способ расчета мощности, когда сила перемещает тело и при этом скорость тела не меняется:

Формулу можно записать в скалярном виде:

$ F \left( H \right) $ – сила, перемещающая тело;

$ \displaystyle v \left( \frac> \right) $ – скорость тела;

$ \alpha $ – угол между вектором силы и вектором скорости тела;

Когда векторы $\vec$ и $\vec$ параллельны, запись формулы упрощается:

Примечание: Такую формулу для расчета мощности можно получить из выражения для работы силы, разделив обе части этого выражения на время, в течение которого работа совершалась (а если точнее, найдя производную обеих частей уравнения).

КПД – коэффициент полезного действия. Обычно обозначают греческим символом $\eta$ «эта». Единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах.

Примечания:

Процент – это дробь, у которой в знаменателе число 100.
КПД — это либо правильная дробь, или дробь, равная единице.

Вычисляют коэффициент $\eta$ для какого-либо устройства, механизма или процесса.

$ \large A_> \left(\text \right)$ – полезная работа;

$\large A_> \left(\text \right)$ – вся затраченная для выполнения работы энергия;

Примечание: КПД часто меньше единицы, так как всегда есть потери энергии. Коэффициент полезного действия не может быть больше единицы, так как это противоречит закону сохранения энергии.

Величина $\eta$ является дробной величиной. Если числитель и знаменатель дроби разделить на одно и то же число, полученная дробь будет равна исходной. Используя этот факт, можно вычислять КПД, используя мощности:

Источник

Основные параметры электродвигателя

Момент электродвигателя

Нормы амортизации: формула расчета с пояснениями. норма амортизации основных средств

Вращающий момент (синонимы: вращательный момент, крутящий момент, момент силы) — векторная физическая величина, равная произведению радиус вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы.

где M – вращающий момент, Нм,
F – сила, Н,
r – радиус-вектор, м

Справка: Номинальный вращающий момент М_ном, Нм, определяют по формуле

где P_ном – номинальная мощность двигателя, Вт,
n_ном — номинальная частота вращения, мин-1

Начальный пусковой момент — момент электродвигателя при пуске.

Справка: В английской системе мер сила измеряется в унция-сила (oz, ozf, ounce-force) или фунт-сила (lb, lbf, pound-force)

1 oz = 1/16 lb = 0,2780139 N (Н)1 lb = 4,448222 N (Н)

момент измеряется в унция-сила на дюйм (oz∙in) или фунт-сила на дюйм (lb∙in)

1 oz∙in = 0,007062 Nm (Нм)1 lb∙in = 0,112985 Nm (Нм)

Мощность электродвигателя

Мощность электродвигателя — это полезная механическая мощность на валу электродвигателя.

Мощность электродвигателя постоянного тока

Механическая мощность

Мощность — физическая величина, показывающая какую работу механизм совершает в единицу времени.

где P – мощность, Вт,
A – работа, Дж,
t — время, с

Работа — скалярная физическая величина, равная произведению проекции силы на направление F и пути s, проходимого точкой приложения силы .

где s – расстояние, м

Для вращательного движения

где – угол, рад,

где – углавая скорость, рад/с,

Таким образом можно вычислить значение механической мощности на валу вращающегося электродвигателя

Справка: Номинальное значение — значение параметра электротехнического изделия (устройства), указанное изготовителем, при котором оно должно работать, являющееся исходным для отсчета отклонений.

Коэффициент полезного действия электродвигателя

Коэффициент полезного действия (КПД) электродвигателя — характеристика эффективности машины в отношении преобразования электрической энергии в механическую.

где – коэффициент полезного действия электродвигателя,
P₁ — подведенная мощность (электрическая), Вт,
P₂ — полезная мощность (), Вт

При этом

потери в электродвигатели обусловлены:
электрическими потерями — в виде тепла в результате нагрева проводников с током;
магнитными потерями — потери на перемагничивание сердечника: потери на вихревые токи, на гистерезис и на магнитное последействие;
механическими потерями — потери на трение в подшипниках, на вентиляцию, на щетках (при их наличии);
дополнительными потерями — потери вызванные высшими гармониками магнитных полей, возникающих из-за зубчатого строения статора, ротора и наличия высших гармоник магнитодвижущей силы обмоток.

КПД электродвигателя может варьироваться от 10 до 99% в зависимости от типа и конструкции.

Международная электротехническая комиссия (International Electrotechnical Commission) определяет требования к эффективности электродвигателей. Согласно стандарту IEC 60034-31:2010 определено четыре класса эффективности для синхронных и асинхронных электродвигателей: IE1, IE2, IE3 и IE4.

где n — частота вращения электродвигателя, об/мин

Момент инерции ротора

Момент инерции — скалярная физическая величина, являющаяся мерой инертности тела во вращательном движении вокруг оси, равна сумме произведений масс материальных точек на квадраты их расстояний от оси

где J – момент инерции, кг∙м2,
m — масса, кг

Справка: В английской системе мер момент инерции измеряется в унция-сила-дюйм (oz∙in∙s2)

1 oz∙in∙s2 = 0,007062 kg∙m2 (кг∙м2)

Момент инерции связан с моментом силы следующим соотношением

где – угловое ускорение, с-2

Справка: Определение момента инерции вращающейся части электродвигателя описано в ГОСТ 11828-86

Номинальное напряжение

Номинальное напряжение (англ. rated voltage) — напряжение на которое спроектирована сеть или оборудование и к которому относят их рабочие характеристики .

Электрическая постоянная времени

Электрическая постоянная времени — это время, отсчитываемое с момента подачи постоянного напряжения на электродвигатель, за которое ток достигает уровня в 63,21% (1-1/e) от своего конечного значения.

где – постоянная времени, с

Механическая характеристика двигателя представляет собой графически выраженную зависимость частоты вращения вала от электромагнитного момента при неизменном напряжении питания.

Нужны ли устройства компенсации в быту?

Кпд электродвигателя и коррекция коэффициента мощности

На первый взгляд в домашней сети не должно быть больших реактивных токов. В стандартном наборе бытовых потребителей преобладают электрическая техника с резистивными нагрузками:

электрочайник (Pf = 1);
лампы накаливания (Pf = 1);
электроплита (Pf = 1) и другие нагревательные приборы;

Коэффициенты мощности современной бытовой техники, такой как телевизор, компьютер и т.п. близки к 1. Ими можно пренебречь.

Но если речь идёт о холодильнике (Pf = 0,65), стиральной машине и микроволновой печи, то уже стоит задуматься об установке синхронных компенсаторов. Если вы часто пользуетесь электроинструментом, сварочным аппаратом или у вас дома работает электронасос, тогда установка устройства компенсации более чем желательна.

Экономический эффект от установки таких устройств ощутимо скажется на вашем семейном бюджете. Вы сможете экономить около 15% средств ежемесячно. Согласитесь, это не так уж мало, учитывая тарифы не электроэнергию.

Попутно вы решите следующие вопросы:

уменьшение нагрузок на индуктивные элементы и на проводку;
улучшение качества тока, способствующего стабильной работе электронных устройств;
понижение уровня высших гармоник в бытовой сети.

Для того чтобы ток и напряжение работали синфазно, устройства компенсации следует размещать как можно ближе к потребителям тока. Тогда реальная отдача индуктивных электроприёмников будет принимать максимальные значения.

Мощность вращающихся объектов

Тюнинг двигателя нива 4х4 увеличение мощности

Для расчета подобной системы применяют формулу:

N = M * w = (2π * M* n)/60,

где:

M – момент силы;
w – угловая скорость, характеризующая вращение;
n – количество оборотов, которое совершает двигатель или другое устройство за 60 секунд.

Приведенные сведения используют с учетом целевого назначения и реальных условий. Так, в термодинамике необходимо помнить о зависимости эффективности системы от температуры окружающей среды. Тепловые потери нагревателя оценивают по соответствующей мощности на единицу площади поверхности. Аналогичным образом поступают при решении механических задач для расчета тяги, КПД, иных рабочих параметров. Как правило, приходится специальным коэффициентом компенсировать трение.

В электрических цепях ток ограничивает сопротивление проводника. Для небольших расстояний при малой мощности тщательные расчеты не нужны. Однако проект магистральной трассы обязательно содержит соответствующие вычисления. На основе полученных результатов делают выводы о среднегодовых экономических показателях. Следует помнить о необходимости учета искажений, которые добавляют при работе с переменным напряжением реактивные нагрузки.

Работа — разность кинетической энергии

Работу можно рассчитать еще одним способом — измеряя кинетическую энергию тела в начале и в конце процесса движения. Рассмотрим такой пример. Пусть автомобиль, движется по горизонтальной прямой и, при этом увеличивает свою скорость (рис. 2). Масса автомобиля 1000 кг. В начале его скорость равнялась 1 м/с. После разгона скорость автомобиля равна 10 метрам в секунду. Найдем работу, которую пришлось проделать, чтобы ускорить этот автомобиль.

Для этого посчитаем энергию движения автомобиля в начале и в конце разгона.

$ E_ \left(\text \right) $ – начальная кинетическая энергия машины;

$ E_ \left(\text \right) $ – конечная кинетическая энергия машины;

$ m \left( \text\right) $ – масса автомобиля;

$ \displaystyle v \left( \frac>\right) $ – скорость, с которой машина движется.

Кинетическую энергию будем вычислять, используя формулу:

Теперь найдем разницу кинетической энергии в конце и вначале разгона.

Значит, работа, которую потребовалось совершить, чтобы разогнать машину массой 1000 кг от скорости 1 м/с до скорости 10 м/с, равняется 49500 Джоулям.

Примечание: Работа – это разность энергии в конце процесса и в его начале. Можно находить разность кинетической энергии, а можно — разность энергии потенциальной.

Определение и формулы мощности

Определение

Мощностью некоторой силы является скалярная физическая величина, которая характеризует скорость произведения работы данной силой. Мощность часто обозначают буквами: N, P.

$$P=\frac{\Delta A}{\Delta t}(1)$$

В том случае, если за равные малые промежутки времени выполняется разная работа, то мощность является переменной во времени.
Тогда вводят мгновенное значение мощности:

где $\delta A$ – элементарная работа, которую выполняет сила,
$\Delta t$ – отрезок времени в течение, которого данная работа была выполнена.
Если мгновенная мощность не является постоянной величиной, то выражение (1) определяет среднюю мощностьза время
$\Delta t$.

Мощность силы можно определить как скалярное произведение силы на скорость, с которой движется точка приложения рассматриваемой силы:

где $F_{\tau}$ – проекция силы
$\bar{F}$ на направление вектора скорости (
$\bar{v}$).

При поступательном движении некоторого тела, имеющего массу m под воздействием силы
$\bar{F}$ мощность можно вычислить, применяя формулу:

В общем случае произвольного перемещения твердого тела суммарная мощность есть алгебраическая сумма мощностей всех сил,
которые действуют на тело:

где $\bar{v}_{i}$ – скорость перемещения точки, к которой приложена сила
$\bar{F}_{i}$.

В случае поступательного движения твердого тела со скоростью $\bar{v}$ мощность можно определить при помощи формулы:

где $\bar{F}$ – главный вектор внешних сил.

Если твердое тело совершает вращение вокруг точки О или вокруг неподвижной оси, которая проходит через точку О, то формулой для счет мощности можно считать выражение:

где $\bar{M}$ – главный момент внешних сил по отношению к точке О,
$\bar{omega}$ – мгновенная угловая скорость вращения тела.

Знак работы силы

Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:

Если α = 0 о , то cosα = 1.
Если 0 о o , то cosα > 0.
Если α = 90 о , то cosα = 0.
Если 90 о o , то cosα о , то cosα = –1.

Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180 о ). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0 о ). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.

Определение мощности электродвигателя по потребляемому току

Мощность двигателя можно определить по потребляемому им току. Для измерения силы тока будем использовать токоизмерительные клещи.

Перед началом измерений предварительно отключаем подачу напряжения на электродвигатель. После этого снимаем крышку с клеммной коробки и расправляем токопроводящие жилы, чтобы обеспечить удобный доступ к ним.

Затем подаем напряжение на двигатель и даем поработать в режиме номинальной нагрузки в течение нескольких минут. Устанавливаем предел измерений на значение «200 А» и токовыми клещами выполняем измерение потребляемого тока на одной из фаз. Далее замеряем напряжение на обмотках с помощью щупов, входящих в комплект токоизмерительных клещей.

Колесо выбора режимов и пределов измерений устанавливаем в позицию для измерения переменного напряжения с пределом в 750 В. Щуп красного цвета присоединяем к гнезду для измерения напряжения, сопротивления и силы тока до десяти Ампер, а черного – к гнезду «COM» . Замеры выполняем между клеммами «U1-V1» или «V1-W1» или «U1-W1» .

Расчет мощности электродвигателя выполняем по формуле:

где S – полная мощность (кВА), I – сила тока (А), U – значение линейного напряжения (кВ).

Замеряем ток на одной из фаз, а также напряжение и подставляем полученные значения в формулу (например, при замере мы получили ток равный 15,2А, а напряжение – 220В):

Важно отметить, что мощность эл. двигателя не зависит от схемы соединения обмоток статора

В этом можно убедиться, выполнив измерения на этом же двигателе, но с обмотками статора, соединенными по схеме «звезда»: измеренный ток будет равен 8,8А, напряжение – 380В. Также подставляем значения в формулу:

По этой формуле мы определили мощность электродвигателя, потребляемую из электрической сети.

Чтобы узнать мощность двигателя на валу, нужно полученное значение умножить на коэффициент мощности двигателя и на коэффициент его полезного действия. Таким образом, формула мощности двигателя выглядит так:

где P – мощность двигателя на валу; S – полная мощность двигателя; сosφ – коэффициент мощности асинхронного электродвигателя; η – КПД двигателя.

Поскольку мы не располагаем точными данными, подставим в формулу средние значения cosφ и КПД двигателя:

Таким образом, мы определили мощность электродвигателя, которая равна 4 кВт.

Мы рассказали о самых надежных методах определения мощности электродвигателя. Вы также можете посмотреть наше видео, в котором подробно показано, как определить мощность электродвигателя.

Оригинал статьи размещен на нашем сайте

Источник

Часто задаваемые вопросы

Как рассчитать мощность двигателя внутреннего сгорания?

Мощность двигателя в кВт можно рассчитать по объему двигателя и оборотах коленвала. Формула расчета мощности двигателя имеет вид: Ne = Vh * Pe * n / 120 (кВт), где: Vh — объём двигателя, см³ n — количество оборотов коленчатого вала за минуту Pe — среднее эффективное давление, Мпа

Какой коэффициент учитывать при расчете мощности двигателя?

Коэффициент мощности (cosϕ) для расчета мощности электродвигателя принимают равным 0,8 для маломощных двигателей (менее 5,5 кВт) или 0,9 для двигателей мощностью свыше 15 кВт.

Как рассчитать мощность двигателя по крутящему моменту?

Для определения мощности двигателя в киловаттах, когда известен крутящий момент, можно по формуле такого вида: P = Mкр * n/9549, где: Mкр – крутящий момент (Нм), n – обороты коленвала (об./мин.), 9549 – коэффициент для перевода оборотов в об/мин.

Как рассчитать мощность двигателя по расходу воздуха?

Рассчитать мощность двигателя в кВт зная его потребления воздуха (при наличии бортового компьютера) можно используя простую схему. Необходимо раскрутить двигатель на третьей передаче до 5500 об/мин (пик крутящего момента) и по показаниям, на тот момент, зафиксировать расход воздуха, а затем разделить то значение на три. В результате такого математического вычисления можно узнать приблизительную мощность двигателя с небольшой погрешностью.

Источник

Примеры решения задач

Задание. Какова мощность (P(t)), развиваемая силой, если она действует на тело, которое имеет массу m и под воздействием приложенной силы движется поступательно. Сила описывается законом: $F(t)=2 t \cdot \bar+3 t^ \bar$

Решение. В качестве основы для решения задачи используем формулу для мощности вида:

Из второго закона Ньютона мы имеем:

$$F=m a \rightarrow a=\frac; v=\int a d t=\int \fracd t=\frac \int F d t(1.2)$$

В выражение (2.2) подставим уравнение, заданное в условии задачи для F(t), имеем:

$$v=\frac \int\left(2 t \cdot \bar+3 t^ \bar\right) d t=\frac\left(t^ \cdot \bar+t^ \bar\right)(1.3)$$

Подставим выражение для скорости из (1.3) в (1.1), получим:

$$P=\left(2 t \cdot \bar+3 t^ \bar\right) \frac\left(t^ \cdot \bar+t^ \bar\right)=\frac\left(2 t^+3 t^\right)$$

Ответ. $P=\frac\left(2 t^+3 t^\right)$

Формула мощности не по зубам? Тебе ответит эксперт через 10 минут!

Задание. Какова мгновенная мощность силы тяжести на высоте h/2. если камень массы m падает с высоты h. Сопротивление воздуха не учитывать.

Решение. Сделаем рисунок.

В качестве основы для решения задачи используем формулу для мгновенной мощности вида:

Сила, действующая на тело – сила тяжести. Она направлена по оси Y, выражение для ее проекции на ось Y запишем как:

В начальный момент времени тело имело скорость равную нулю, тогда скорость тела в проекции на ось Y можно вычислить, используя выражение:

Найдем момент времени, в который тело окажется на половине высоты (y=h/2), применим уравнение, которое описывает равноускоренное движение (из начальных условий y=0, v=0):

Используем выражения (2.2), (2.3), (2.4) подставим в (2.1), получим искомую мгновенную мощность силы тяжести на половине пути свободно падающего тела:

Ответ. $P=m \sqrt h>$

Источник

Мощность электрического тока

Для того, чтобы это показать что к чему, мы возьмем две лампы на 12 Вольт, но разной мощности. На блоке питания выставляю также 12 Вольт и собираю все это дело по схеме, которая мелькала в начале статьи

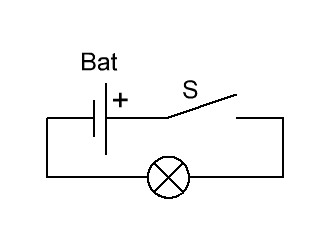
Мой блок питания может выдать в нагрузку 150 Ватт, не парясь. Беру лампочку от мопеда и цепляю ее к блоку питания

Смотрим потребление тока. 0,71 Ампер

Высчитываем сопротивление раскаленной нити лампочки из закона Ома I=U/R, отсюда R=U/I=12/0,71=16,9 Ом.

Беру галогенную лампу от фары авто и также цепляю ее к блоку питания

Смотрим потребление. 4,42 Ампера

Аналогично высчитываем сопротивление нити лампы. R=U/I=12/4,42=2,7 Ом.

А теперь давайте посчитаем, какая лампочка больше всех Ватт “отбирает” у источника питания. Вспоминаем школьную формулу P=UI. Итак, для маленькой лампочки мощность составит P=12×0,71=8,52 Ватта. А для большой лампочки мощность будет Р=12х4,42=53 Ватта. Ого! У нас получилось, что лампочка, которая обладала меньшим сопротивлением, на самом деле очень даже прожорливая.

Итак, если кто не помнит, что такое мощность, могу напомнить. Мощность – это отношение какой-то полезной работы к времени, в течение которого эта работа совершалась. Например, надо вскопать яму определенных размеров. Вы с лопатой, а ваш друг – на экскаваторе:

Кто быстрее справится с задачей за одинаковый промежуток времени? Разумеется экскаватор. В этом случае, можно сказать, что его мощность намного больше, чем мощность человека с лопатой.

А теперь представьте, что нам надо полностью под ноль сточить эту железяку:

Подумайте вот над таким вопросом… У нас есть в запасе 5 мин и нам надо сточить железяку по-максимому. В каком случае железяка сточится быстрее всего: если прижимать ее к абразивному кругу со всей дури, прижимать слегка, либо прижимать в полсилы? Не забывайте, что у нас абразивный круг подцеплен к валу, который крутит поток воды в трубе. И да, труба у нас небольшого диаметра.

Кто ответил, что если прижимать в полсилы, то оказался прав. Железяка в этом случае сточится быстрее. Если прижимать ее со всей дури, то можно вообще остановить круг. Еще раз, что у нас такое мощность? Полезная работа, совершаемая за какой-то промежуток времени. А в нашем опыте полезная работа это и есть стачивание железяки по максималке. Также не забывайте и тот момент, что если мы будем слегка прижимать железяку, то мы будем ее стачивать пол дня. Поэтому, золотая середина – это давить железяку в полсилы.

Ну вот мы и снова переходим к электронике 😉

Поток воды – сила тока, давление в трубе – напряжение, давление железяки на круг – сопротивление. И что в результате мы получили? А то, что лампочка с меньшим сопротивлением обладает большей мощностью, чем лампочка с большим сопротивлением. Не трудно догадаться, если просто посмотреть на фото, но вживую эффект лучше

Но обязательно ли то, что чем меньше сопротивление, тем больше мощности выделяется на нагрузке? Конечно же нет. Во всем нужен расчет, как и в прошлом опыте, где мы стачивали железяку за определенное время.

И еще один фактор, конечно, тоже надо учитывать. Это давление в трубе. Прикиньте, точим-точим мы железяку, и вдруг давление в трубе стало повышаться. Может быть переполнилась башня, или кто-то открыл краник на полную катушку. Что станет с наждаком? Его обороты ускорятся, так как сила потока воды в трубе увеличится, а следовательно, мы еще быстрее сточим нашу железку.

Мощность

Мощность – это работа, совершенная за одну секунду (энергия, затраченная за 1 сек).

Расчет работы осуществляем, используя любую из формул:

\[ \large A = \Delta E_

Разделив эту работу на время, в течение которого она совершалась, получим мощность.

Мощность переменная, когда в некоторые интервалы времени совершалось больше работы.

Еще одна формула для расчета мощности

Есть еще один способ расчета мощности, когда сила перемещает тело и при этом скорость тела не меняется:

Формулу можно записать в скалярном виде:

$ F \left( H \right) $ – сила, перемещающая тело;

$ \displaystyle v \left( \frac> \right) $ – скорость тела;

$ \alpha $ – угол между вектором силы и вектором скорости тела;

Когда векторы $\vec$ и $\vec$ параллельны, запись формулы упрощается:

Примечания:

Процент – это дробь, у которой в знаменателе число 100.
КПД — это либо правильная дробь, или дробь, равная единице.

Вычисляют коэффициент $\eta$ для какого-либо устройства, механизма или процесса.

$ \large A_> \left(\text \right)$ – полезная работа;

$\large A_> \left(\text \right)$ – вся затраченная для выполнения работы энергия;

Источник